3.4. Aplicaciones en la Biologia.
Uno de los modelos clásicos que se usan mucho en la Biología, es el referido a modelo de crecimiento demográfico, el mismo fué estudiado por el economista inglés Thomas Malthus en el siglo pasado, alrededor del año 1978. El modelo malthusiano, como normalmente se le conoce, es formulado matemáticamente suponiendo que la tasa de crecimiento poblacional es proporcional a la población total, es decir, que mientras mayor sea la población, mayor será el crecimiento de la población, lo cuál en términos matemáticos lo podemos expresar de la siguiente manera:

donde k es la constante de proporcionalidad poblacional.
Es de hacer notar que este modelo poblacional es un modelo muy sencillo, pero que no toma en cuenta algunos parámetros que son de importancia cuando se trata de predecir la población humana, ya que existen otros parámetros que pueden hacer crecer o disminuir la población humana, como por ejemplo, la inmigración y la emigración. Sin embargo, este modelo poblacional, predijo con una buena exactitud la población de los Estados Unidos, entre los años 1790 hasta los años 1860, donde quizás estos parámetros que antes nombramos nos eran de mucha influencia.
Pero en la Biología, este modelo malthusiano es usado con bastante regularidad para estudiar el crecimiento de poblaciones de bacterias y animales, para intervalos de tiempo pequeños.
Otro de los modelos de interés, es muy similar al malthusiano, es el de diseminación o propagación de enfermedades o plagas. Este modelo, es normal pensar que la tasa con la que se propaga la enfermedad o plaga no sea proporcional a la cantidad de personas infectadas, es por ello, que podemos describirlo como que la tasa de propagación de la enfermedad es proporcional al producto de la cantidad de personas infectadas por las que no han sido infectadas aún en la población, lo cuál en términos matemáticos lo podemos escribir de la siguiente manera:

donde k es la constante de proporcionalidad, pero si suponemos que a una población de n individuos, se introduce una persona infectada, entonces la ecuación diferencial anterior la podemos escribir en función de solamente la población infectada y su tasa de propagación como sigue:
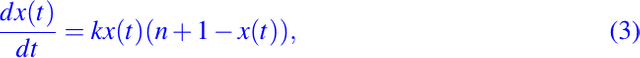
Existen numerosos modelos matematicos de diversa indole que se utilizan hoy en dıa para el estudio de problemas en Biologıa y otras ciencias experimentales; sus objetivos principales son describir, explicar y predecir fenomenos y procesos en dichas areas. La gran parte de tales modelos matematicos se expresa mediante ecuaciones diferenciales.
El objetivo de este tema es describir brevemente algunos de los conceptos basicos relacionados con las ecuaciones diferenciales ordinarias, mostrar tecnicas elementales de su resolucion, ası como exponer ejemplos practicos de aplicaciones.
Una ecuacion diferencial es una ecuacion en que la incognita es una funcion: no el valor de la funcion en uno o varios puntos, sino la funcion en sı misma. Ademas, la ecuacion involucra no solo la funcion (incognita), sino tambien sus derivadas hasta un cierto orden.
Cuando la incognita es una funcion de una sola variable se dice que la ecuacion es ordinaria, debido a que la o las derivadas que aparecen son derivadas ordinarias (por contraposicion a las derivadas parciales de las funciones de varias variables).
Por ejemplo, y 0 (t) = −y(t)
es una ecuacion diferencial ordinaria (edo) de primer orden, ya que la maxima derivada que aparece en ella es la de primer orden. Si no resulta confuso se suele escribir tambien esta ecuacion en la forma y 0 = −y, omitiendo la menci´on expresa a la dependencia de y respecto a la variable independiente, t
Resolver esta ecuacion consiste en encontrar una o varias funciones y = y(t) que verifiquen la igualdad y 0 (t) = −y(t), para todo t perteneciente a un cierto intervalo I. Una tal funcion se dice que es una solucion de la edo en el intervalo I.
Con caracter general, una ecuacion diferencial ordinaria de primer orden se escribe: y 0 = f(t, y)
y se dice que y = y(t) es solucion en I de esta ecuacion si se verifica

