1.1.Definiciones Basicas y clasificacion de las ecuaciones diferenciales.

Definicion:Una ecuación diferencial es una ecuación que involucra derivadas (o diferenciales) de una función desconocida de una o más variables. Si la función desconocida depende sólo de una variable, la ecuación se llama una ecuación diferencial ordinaria. Sin embargo, si la función desconocida depende de más de una variable la ecuación se llama una ecuación diferencial parcial.

Un ejemplo de ecuación diferencial ordinaria es:

La variable independiente (v. i) es x

La variable dependiente (v. d) es y

Un ejemplo de ecuación diferencial parcial es:

La variable independiente (v. i) es "x" y "y"

La variable dependiente (v. d) es V

Orden de una ecuacion diferencial:El orden de una ecuación diferencial está dado por el orden mayor de su derivada.

Ejemplo

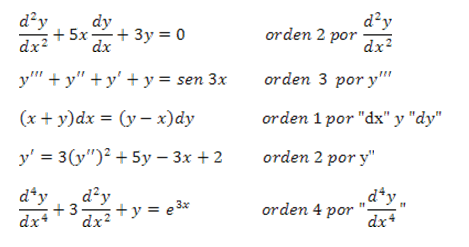
Grado de una Ecuacion Diferencial:El grado de una ecuación diferencial está dado por el exponente del mayor orden de su derivada.

Ejemplos:

Determinar el orden y grado de las siguientes ecuaciones diferenciales ordinarias.

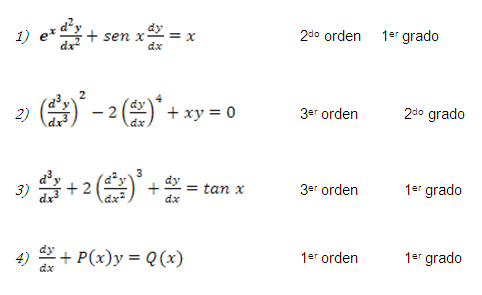
Clasificación de las ecuaciones diferenciales.

Las ecuaciones diferenciales se clasifican en función de:

-TIPO.  

-ORDEN. 

-LINEALIDAD

Clasificación por tipo: Si una ecuación diferencial contiene sólo derivadas ordinarias de una o mas variables dependientes con respecto a una sola variable independiente se dice que es una ecuación diferencial ordinaria. Algunos ejemplos de ecuaciones diferenciales ordinarias:

Si una ecuación diferencial contiene derivadas parciales de una o mas variables dependientes con respecto a una o más variables independientes se dice que es una ecuación diferencial parcial. 

Algunos ejemplos de ecuaciones diferenciales parciales:

Clasificación según el orden:El orden de una ecuación diferencial (ya sea ordinaria o parcial) es el orden de la derivada mayor en la ecuación.

Es una ecuación diferencial ordinaria de segundo orden.

- Una ecuación diferencial ordinaria de n-ésimo orden se puede expresar mediante la forma general: F(x, y, y´, y´´, . . ., y(n))=0 Donde F es una función de valores reales de n+2 variables x, y, y´, y´´, ..., y(n)

- Es posible despejar de una ecuación diferencial ordinaria en forma única la derivada superior y(n) en términos de las n+1 variables restantes. La ecuación diferencial: 

Donde f es una función continua de valores reales, se denomina forma normal.

Clasificación según la linealidad:Se dice que una ecuación diferencial ordinaria de orden n es lineal si F es lineal en y, y´, y´´, . . ., y(n). Esto significa que una ecuación diferencial ordinaria de orden n es lineal cuando:

-En las ecuaciones diferenciales lineales de primero y segundo orden (n=1 y n=2)