Aplicaciones de Ecuaciones Diferenciales.
A continuación se dan aplicaciones físicas de las ecuaciones diferenciales de segundo orden. Hay tambien muchas aplicaciones de ecuaciones diferenciales de primer orden.
Movimientos armonico simple:
Péndulo Simple:
Ecuación Acimutal, átomo de hidrógeno:
Perfil de Velocidad en un flujo de fluido.
Aplicaciones de E.D. Homogénea de Primer Orden.
La forma general de la solución de una ecuación diferencial homogénea se puede aplicar a una gran cantidad de problemas físicos.
Variación de la Presión Barométrica con la altitud:
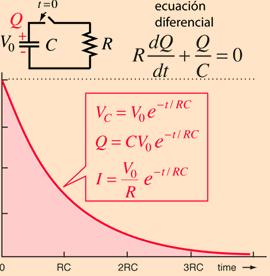
Descarga de un condensador:
Otras aplicaciones en la Fisica.Ecuaciones de Euler-Lagrange en mecánica clásicaEcuaciones de Hamilton en mecánica clásicaRadiactividad en física nuclearLey de enfriamiento de Newton en termodinámicaEcuación de ondaEcuación de calor en termodinámicaEcuación de Laplace, que define las funciones armónicasEcuación de PoissonEcuación geodésicaEcuaciones de Navier-Stokes en fluidodinámicaEcuación de difusión en procesos estocásticosEcuación de convección-difusión en fluidodinámicaEcuaciones de Cauchy-Riemann en análisis complejoEcuación de Poisson-Boltzmann en dinámica molecularEcuaciones de Saint-VenantEcuación diferencial universalEcuaciones de Lorenz cuyas soluciones exhiben un flujo caótico.